Multiplicação de Matrizes em Python: Um Guia Completo
Neste guia, você explorará detalhadamente a multiplicação de matrizes utilizando Python. Abordaremos desde os fundamentos teóricos até a implementação prática, garantindo um aprendizado completo e eficaz.
Inicialmente, você compreenderá a condição essencial para que a multiplicação de matrizes seja considerada válida, e então, desenvolverá uma função personalizada em Python para realizar essa operação. Em seguida, exploraremos como alcançar o mesmo resultado através de compreensões de lista aninhadas.
Por fim, você avançará para o uso do NumPy, uma biblioteca poderosa, e suas funções integradas, que oferecem uma forma otimizada e eficiente de efetuar a multiplicação de matrizes.
Verificando a Validade da Multiplicação de Matrizes
Antes de mergulharmos no código Python, vamos recordar os princípios básicos que regem a multiplicação de matrizes.
A multiplicação de duas matrizes, digamos A e B, é considerada válida somente se o número de colunas da matriz A coincidir com o número de linhas da matriz B.
Você já deve ter se deparado com essa regra anteriormente. Mas, você já se questionou sobre a razão por trás dessa condição?
A resposta reside na própria mecânica da multiplicação de matrizes. Observe a ilustração a seguir:
Neste cenário genérico, a matriz A possui m linhas e n colunas, enquanto a matriz B tem n linhas e p colunas.
Qual a Dimensão da Matriz Resultante?
O elemento localizado no índice (i, j) da matriz resultante C é, na verdade, o produto escalar entre a linha i da matriz A e a coluna j da matriz B.
Portanto, para obter um elemento específico na matriz resultante C, é necessário calcular o produto escalar da linha e coluna correspondentes das matrizes A e B.
Ao repetir este processo, você obterá a matriz produto C com dimensões mxp, ou seja, com m linhas e p colunas, como demonstrado a seguir.
O produto escalar, ou produto interno, entre dois vetores, a e b, é expresso pela seguinte equação:

Vamos recapitular os pontos principais:
- É fundamental notar que o produto escalar só é definido entre vetores com o mesmo comprimento.
- Consequentemente, para que o produto escalar entre uma linha e uma coluna seja válido durante a multiplicação de matrizes, ambas devem ter a mesma quantidade de elementos.
- No exemplo genérico apresentado, cada linha da matriz A possui n elementos, assim como cada coluna da matriz B.
Observando mais atentamente, percebemos que n corresponde ao número de colunas da matriz A e, simultaneamente, ao número de linhas da matriz B. Esta é exatamente a razão pela qual o número de colunas da matriz A deve ser idêntico ao número de linhas da matriz B.
Espero que agora você tenha uma compreensão clara da condição necessária para a validação da multiplicação de matrizes, bem como do processo de obtenção de cada elemento da matriz resultante.
Vamos prosseguir com a escrita do código Python para realizar a multiplicação de duas matrizes.
Criando uma Função Personalizada em Python para Multiplicar Matrizes
Inicialmente, desenvolveremos uma função personalizada para efetuar a multiplicação de matrizes.
Esta função deverá realizar as seguintes operações:
- Receber duas matrizes, A e B, como entradas.
- Verificar se a multiplicação entre A e B é válida.
- Caso seja válida, multiplicar as matrizes A e B e retornar a matriz produto C.
- Caso contrário, retornar uma mensagem de erro indicando que a multiplicação entre A e B não é possível.
Passo 1: Vamos gerar duas matrizes de inteiros utilizando a função random.randint() do NumPy. Alternativamente, você também pode definir matrizes utilizando listas aninhadas em Python.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matrix A:n {A}n")
print(f"Matrix B:n {B}n")
# Output
Matrix A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matrix B:
[[2 2]
[5 7]
[4 4]]
Passo 2: Agora, definiremos a função `multiply_matrix(A,B)`. Esta função receberá as matrizes A e B como entradas e retornará a matriz produto C, caso a multiplicação seja possível.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(A.shape[0]):
for col in range(B.shape[1]):
for elt in range(A.shape[1]):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Desculpe, não é possível multiplicar A e B."
Analisando a Estrutura da Função
Vamos agora detalhar a estrutura da função.
Declarando C como variável global: Em Python, por padrão, todas as variáveis dentro de uma função têm escopo local. Isso significa que não podem ser acessadas fora da função. Para que a matriz produto C seja acessível externamente, precisamos declará-la como uma variável global. Isso é feito através da inclusão do qualificador `global` antes do nome da variável.
Verificando a validade da multiplicação de matrizes: Utilizamos o atributo `shape` para verificar se a multiplicação entre A e B é possível. Para qualquer array `arr`, `arr.shape[0]` e `arr.shape[1]` retornam o número de linhas e colunas, respectivamente. Portanto, `A.shape[1] == B.shape[0]` verifica se a condição para a multiplicação de matrizes é satisfeita. A matriz produto só será calculada caso essa condição seja verdadeira, caso contrário, a função retornará uma mensagem de erro.
Utilizando loops aninhados para realizar os cálculos: Para calcular os elementos da matriz resultante, precisamos iterar sobre as linhas da matriz A, o que é realizado pelo loop `for` externo. O loop interno nos ajuda a percorrer as colunas da matriz B. O loop mais interno é utilizado para acessar cada elemento dentro da coluna selecionada.
▶️ Agora que compreendemos o funcionamento da função em Python para multiplicar matrizes, vamos executá-la com as matrizes A e B que geramos anteriormente.
multiply_matrix(A,B)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Como a multiplicação entre A e B é válida, a função `multiply_matrix()` retorna a matriz produto C.
Multiplicação de Matrizes com Compreensão de Lista Aninhada em Python
Na seção anterior, você aprendeu a criar uma função personalizada para multiplicar matrizes em Python. Agora, exploraremos como usar compreensões de lista aninhadas para alcançar o mesmo objetivo.
A seguir, apresentamos a compreensão de lista aninhada utilizada para multiplicar matrizes:
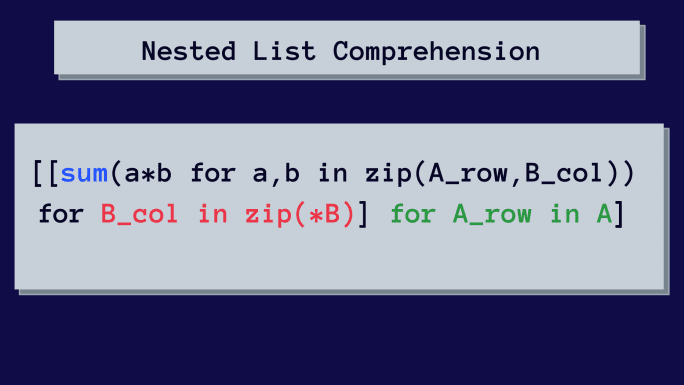
Inicialmente, isso pode parecer um pouco complexo, mas vamos analisar a compreensão de lista aninhada passo a passo.
Vamos focar em uma compreensão de lista por vez para entender seu funcionamento.
Utilizaremos o seguinte modelo geral para compreensão de lista:
[<do-this> for <item> in <iterable>] where, <do-this>: a operação ou expressão que você deseja realizar <item>: cada item sobre o qual a operação será executada <iterable>: o iterável (lista, tupla, etc.) que está sendo percorrido
▶️ Consulte nosso guia sobre Compreensão de listas em Python para uma compreensão mais aprofundada.
Antes de prosseguirmos, lembre-se de que nosso objetivo é construir a matriz resultante C linha por linha.
Entendendo a Compreensão de Lista Aninhada
Etapa 1: Calculando um único valor na matriz C
Dada a linha i da matriz A e a coluna j da matriz B, a expressão abaixo fornece o elemento na posição (i, j) da matriz C.
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) retorna um iterador de tuplas # Se A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) retorna (a1, b1), (a2, b2), e assim por diante
Se i = j = 1, a expressão retornará o elemento c_11 da matriz C. Assim, é possível obter um elemento de uma linha desta forma.
Passo 2: Construindo uma linha na matriz C
Nosso próximo objetivo é construir uma linha completa.
Para a linha 1 da matriz A, é necessário percorrer todas as colunas da matriz B para obter uma linha completa na matriz C.
Retorne ao modelo de compreensão de lista.
- Substitua <do-this> pela expressão da etapa 1, pois é o cálculo desejado.
- Substitua <item> por B_col—cada coluna da matriz B.
- Por fim, substitua <iterable> por zip(*B)—a lista contendo todas as colunas na matriz B.
E aqui está a primeira compreensão de lista:
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * é o operador de desempacotamento # zip(*B) retorna uma lista das colunas da matriz B
Passo 3: Construindo todas as linhas e obtendo a matriz C
Em seguida, preencheremos a matriz produto C calculando as demais linhas.
Para isso, é preciso percorrer todas as linhas da matriz A.
Volte novamente à compreensão de lista e faça o seguinte:
- Substitua <do-this> pela compreensão de lista da etapa 2. Lembre-se que na etapa anterior calculamos uma linha completa.
- Agora, substitua <item> por A_row—cada linha da matriz A.
- E o <iterable> será a própria matriz A, que será percorrida por suas linhas.
E aqui está nossa compreensão de lista aninhada final.🎉
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Agora é hora de verificar o resultado! ✔
# Converta para um array NumPy utilizando np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Output:
[[ 89 107]
[ 47 49]
[ 40 44]]
Analisando com atenção, vemos que o resultado é equivalente aos loops `for` aninhados que vimos anteriormente, porém de forma mais concisa.
Também é possível realizar essa operação de forma mais eficiente utilizando algumas funções internas. Vamos explorá-las na próxima seção.
Utilizando NumPy matmul() para Multiplicação de Matrizes em Python
A função `np.matmul()` recebe duas matrizes como entrada e retorna o produto, caso a multiplicação entre elas seja válida.
C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Observe como este método é mais simples e direto do que os dois métodos que aprendemos anteriormente. Na verdade, ao invés de `np.matmul()`, você também pode usar o operador `@` que possui a mesma funcionalidade. Iremos explorar esse operador a seguir.
Como Utilizar o Operador @ em Python para Multiplicar Matrizes
Em Python, o operador `@` é um operador binário que realiza a multiplicação de matrizes.
Ele opera sobre duas matrizes, geralmente arrays NumPy N-dimensionais, e retorna a matriz produto resultante.
Observação: É necessário ter o Python versão 3.5 ou superior para utilizar o operador `@`.
Veja como ele pode ser utilizado:
C = A @ B
print(C)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Note que a matriz produto C é idêntica à que obtivemos anteriormente.
É Possível Utilizar np.dot() para Multiplicar Matrizes?
Caso você já tenha se deparado com algum código que utiliza `np.dot()` para multiplicar matrizes, entenda como ele funciona:
C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Você verá que `np.dot(A, B)` também retorna a matriz produto esperada.
Entretanto, conforme a documentação do NumPy, você deve usar `np.dot()` apenas para calcular o produto escalar de dois vetores unidimensionais e não para a multiplicação de matrizes.
Lembre-se que, conforme discutido anteriormente, o elemento na posição (i, j) da matriz produto C corresponde ao produto escalar da linha i da matriz A e da coluna j da matriz B.
Como o NumPy aplica implicitamente essa operação de produto escalar a todas as linhas e colunas, você obtém a matriz produto resultante. No entanto, para manter a clareza e evitar ambiguidades em seu código, é recomendado utilizar `np.matmul()` ou o operador `@`.
Conclusão
🎯 Neste guia, você aprendeu os seguintes conceitos:
- A condição para que a multiplicação de matrizes seja válida: o número de colunas da matriz A deve ser igual ao número de linhas da matriz B.
- Como desenvolver uma função personalizada em Python que verifica a validade da multiplicação de matrizes e retorna a matriz produto. Essa função utiliza loops `for` aninhados.
- Como utilizar compreensões de lista aninhadas para multiplicar matrizes. Essa abordagem é mais concisa do que o uso de loops `for`, mas pode ser menos legível.
- Como utilizar a função interna do NumPy `np.matmul()` para multiplicar matrizes, e como essa abordagem é a mais eficiente em termos de desempenho.
- Você também aprendeu sobre o operador `@` para multiplicar duas matrizes em Python.
Com isso, concluímos nossa análise sobre a multiplicação de matrizes em Python. Como próximos passos, você pode aprender como verificar se um número é primo em Python ou explorar problemas interessantes envolvendo strings em Python.
Bons estudos! 🎉