A organização de listas de dados é essencial no desenvolvimento de aplicações, facilitando a exibição e a busca de informações. Não surpreende que programadores experientes dominem a arte de ordenar arrays. Este artigo explora alguns dos algoritmos mais empregados para essa finalidade em JavaScript.
O que é Ordenação e Qual a Sua Relevância?
Fonte: Remover respingo
Ordenação, nesse contexto, refere-se ao processo de organizar dados de acordo com uma ordem específica, seja ela crescente ou decrescente. Em JavaScript, a capacidade de ordenar arrays é vital, pois permite apresentar dados de maneira mais intuitiva. Por exemplo, pode-se querer visualizar arquivos ordenados pelos mais recentes ou produtos listados por preço. Além disso, a ordenação é fundamental para algoritmos de busca binária, que funcionam apenas em dados pré-ordenados.
Embora existam funções e bibliotecas que simplificam a ordenação, entender os mecanismos internos é valioso para entrevistas de emprego ou quando se necessita escrever código de baixo nível.
Algoritmos de Ordenação de Array em JavaScript
Ordenação por Bolha (Bubble Sort)

O Bubble Sort destaca-se pela simplicidade de compreensão e implementação. A lógica reside em percorrer o array repetidamente, comparando elementos adjacentes e trocando-os de lugar se estiverem na ordem incorreta. O número de passagens é igual ao número de elementos do array. A cada passagem, o maior elemento “borbulha” para a extremidade direita do array. Abaixo, o pseudocódigo para ordenar números em ordem ascendente:
1. Seja n o número de elementos no array. 2. Repita n vezes, usando i como contador de loops: a. Percorra o array do segundo elemento até o (n - i)-ésimo elemento. b. Se o elemento anterior for maior que o atual, troque-os.
A tradução desse pseudocódigo para JavaScript resulta em:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
Para um entendimento mais profundo do processo, sugiro adicionar instruções `console.log` dentro dos loops, permitindo acompanhar a evolução do array a cada passagem.
O código abaixo exibe uma versão modificada da função `sort` com `console.log`s, juntamente com um exemplo de array não ordenado:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
O resultado da execução desse código será:

O Bubble Sort apresenta uma complexidade de tempo de O(n^2), pois executa n passagens, que iteram pelo array a cada passagem. Isso o torna ineficiente para grandes conjuntos de dados. No entanto, sua complexidade de espaço é O(1), já que as modificações são feitas diretamente no array original.
Ordenação por Inserção (Insertion Sort)

O Insertion Sort é outro algoritmo popular para ordenar arrays em JavaScript. A ideia é escolher um elemento (chamado `num`) e movê-lo para a esquerda até que todos os elementos à sua esquerda sejam menores que ele. Se repetirmos esse processo do segundo elemento até o último, o array estará ordenado. Veja o pseudocódigo:
1. Seja n o número de elementos no array.
2. Repita i de 1 até n - 1 (iniciando do segundo elemento):
a. Defina currentElement como array[i].
b. Defina j como i - 1.
c. Enquanto j >= 0 e array[j] > current_element:
i. Mova array[j] para array[j+1].
ii. Decremente j em 1.
d. Defina array[j+1] como current_element.
E a implementação em JavaScript:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
A inclusão de `console.log`s também facilita a visualização do processo. O código abaixo ilustra o funcionamento do Insertion Sort:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
const array = [4, 1, 2, 5, 3];
sort(array);
A execução desse código produzirá o seguinte resultado:
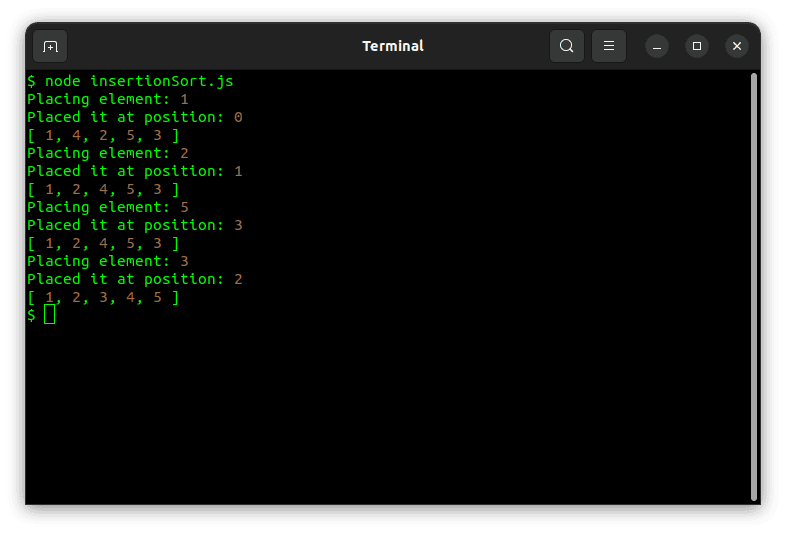
Ordenação por Mistura (Merge Sort)

Diferentemente do Insertion Sort e do Bubble Sort, que apresentam um desempenho quadrático, o Merge Sort opera em um tempo quase linear, com complexidade de O(n * log(n)).
O Merge Sort adota a estratégia de “dividir para conquistar”. O array é subdividido recursivamente em arrays menores, até que cada um contenha apenas um elemento. Em seguida, esses arrays são combinados, de forma ordenada.
A subdivisão é recursiva, para permitir que o array seja remontado. Na fase de combinação, os subarrays são mesclados de forma ordenada. A mesclagem é realizada de maneira semelhante à mesclagem de dois arrays já ordenados. Abaixo, o pseudocódigo desse processo:
1. Se o comprimento do array for menor ou igual a 1, retorne o array (caso base).
2. Encontre o índice do meio:
a. Defina mid como a parte inteira de (comprimento do array / 2).
3. Divida o array em dois subarrays:
a. Crie leftArray e copie a primeira metade do array (do índice 0 até mid).
b. Crie rightArray e copie a segunda metade do array (de mid+1 até o final).
4. Chame recursivamente MergeSort em leftArray.
5. Chame recursivamente MergeSort em rightArray.
6. Mescle os dois subarrays ordenados:
a. Crie um resultArray vazio.
b. Enquanto leftArray e rightArray não estiverem vazios:
i. Se o primeiro elemento de leftArray for menor ou igual ao primeiro elemento de rightArray, adicione-o a resultArray.
ii. Caso contrário, adicione o primeiro elemento de rightArray a resultArray.
c. Adicione quaisquer elementos restantes em leftArray a resultArray (se houver).
d. Adicione quaisquer elementos restantes em rightArray a resultArray (se houver).
7. Retorne resultArray.
A implementação em JavaScript seria:
function sort(array) {
// Caso base para interromper a subdivisão do array
if (array.length == 1) {
return array;
}
// Encontrando o ponto médio do array
const m = Math.round(array.length / 2);
// Dividindo o array em duas metades
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Chamando o merge sort recursivamente
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Retornando um array mesclado e ordenado
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Mesclando duas listas ordenadas
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Ao executar o código com um array de exemplo, ele deverá funcionar corretamente.
Ordenação Rápida (Quick Sort)

Semelhante ao Merge Sort, o Quick Sort também emprega a estratégia de “dividir para conquistar”. O algoritmo escolhe um elemento pivô e move todos os elementos maiores que o pivô para a direita e os menores para a esquerda. Após essa etapa, o pivô estará em sua posição correta.
Para movimentar os elementos em relação ao pivô, o algoritmo inicia transferindo o pivô para o final do array.
Em seguida, um ponteiro percorre o array da esquerda para a direita, buscando o primeiro número maior que o pivô. Simultaneamente, outro ponteiro percorre o array da direita para a esquerda, buscando o primeiro número menor que o pivô. Quando ambos os números são localizados, eles são trocados. Esse processo é repetido até que o ponteiro da esquerda se torne maior que o ponteiro da direita.
Ao interromper o loop, o maior dos dois últimos números trocados é trocado com o pivô. Neste ponto, o pivô estará na posição correta; os números menores que ele estarão à esquerda, enquanto os maiores estarão à direita.
Esse procedimento é repetido recursivamente para os subarrays à esquerda e à direita do pivô até que os subarrays tenham apenas um elemento.
Segue o pseudocódigo para a ordenação rápida:
1. Se lessThanPointer for menor que greaterThanPointer:
a. Escolha um elemento pivô do array.
b. Mova os elementos de modo que os menores fiquem à esquerda e os maiores à direita.
c. Chame recursivamente Quicksort no subarray esquerdo.
d. Chame recursivamente Quicksort no subarray direito.
E a sua conversão para JavaScript:
function sort(array, low, high) {
if (low < high) {
// Escolhe o índice do pivô e particiona o array
const pivotIndex = move(array, low, high);
// Ordena recursivamente os subarrays à esquerda e à direita do pivô
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Seleciona o elemento pivô (neste caso, o último elemento)
const pivotElement = array[high];
// Inicializa o índice para o elemento menor
let i = low - 1;
for (let j = low; j < high; j++) {
// Se o elemento atual for menor ou igual ao pivô, troca-o com o elemento no índice i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Troca o elemento pivô para sua posição correta
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Retorna o índice do elemento pivô
return i + 1;
}
A ordenação de um array de exemplo com Quick Sort em Node.js deve gerar o seguinte resultado:
Na melhor das hipóteses, o Quicksort apresenta um desempenho em tempo quase linear. O uso de espaço também escala logaritmicamente. Portanto, é relativamente eficiente em comparação com outros algoritmos de ordenação de arrays em JavaScript.
Dicas para Suas Entrevistas de Programação
❇️ A prática é fundamental. Ela ajuda a memorizar diversos algoritmos, mas o mais importante é que aprimora suas habilidades de resolução de problemas e pensamento computacional. Você também pode praticar em plataformas como LeetCode e AlgoExpert.
❇️ Tente resolver o problema por conta própria primeiro. Em vez de ir direto para a solução, esforce-se para resolvê-lo, pois isso aprimora suas capacidades de resolução de problemas.
❇️ Se um problema estiver demorando muito, vá direto para a solução; você ainda pode aprender o método de resolução. A maioria das plataformas oferece soluções. O ChatGPT ou o Google Bard também são úteis para esclarecer conceitos.
❇️ Além disso, não comece a escrever código imediatamente; utilize um quadro branco para rascunhar suas soluções e refletir sobre elas antes de escrever o código. O pseudocódigo também é uma forma eficiente de anotar ideias rapidamente.
Conclusão
Neste artigo, exploramos os algoritmos de ordenação mais populares. Aprender todos eles pode parecer desafiador inicialmente. Por isso, recomenda-se sempre consultar diversas fontes de informação em vez de se basear em apenas uma. Boa programação!
Em seguida, veja como entender a função `sorted` em Python.