Explorando Algoritmos de Ordenação: Uma Análise Detalhada
A ordenação é uma operação fundamental na programação. A escolha do algoritmo adequado é crucial para otimizar o tempo de execução, especialmente quando lidamos com grandes volumes de dados.
Neste artigo, vamos explorar diversos algoritmos de ordenação, desde os mais básicos até os mais eficientes.
Apresentaremos cada algoritmo detalhadamente, acompanhado de exemplos práticos de implementação em Python. Essa linguagem foi escolhida pela sua clareza e facilidade de adaptação para outros contextos. O foco principal é a lógica dos algoritmos, não a sintaxe específica da linguagem.
A jornada pelos algoritmos de ordenação será organizada de forma didática, começando pelos métodos menos eficientes e progredindo até os mais sofisticados. Portanto, acompanhe o artigo e coloque o conhecimento em prática.
Vamos agora mergulhar no mundo dos algoritmos de ordenação.
Ordenação por Inserção: Simplicidade e Eficiência Limitada
A ordenação por inserção destaca-se pela simplicidade em sua implementação, sendo fácil de compreender e programar. No entanto, sua eficiência é limitada, especialmente em conjuntos de dados extensos. Geralmente, não é a melhor opção para arrays de grande escala.
O algoritmo de inserção organiza o array em duas partes: uma ordenada e outra não ordenada. Inicialmente, a parte ordenada contém apenas o primeiro elemento do array. Em cada iteração, um elemento da parte não ordenada é selecionado e inserido na posição correta dentro da parte ordenada.
Para facilitar a compreensão, acompanhe a ilustração visual do processo de ordenação por inserção passo a passo com um exemplo:
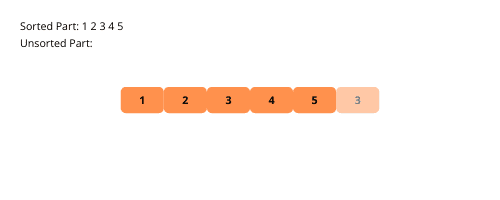
Vejamos agora os passos para implementar a ordenação por inserção:
- Inicialize o array com valores fictícios (inteiros).
- Percorra o array a partir do segundo elemento.
- Armazene o índice e o valor do elemento atual em variáveis temporárias.
- Inicie um loop que retroceda até o início do array ou até encontrar um elemento menor que o atual.
- Desloque o elemento anterior para a posição atual.
- Diminua o índice atual.
- Insira o elemento atual na posição correta.
A complexidade de tempo da ordenação por inserção é de O(n²), enquanto sua complexidade de espaço é O(1).
Com isso, o array está ordenado. Vamos agora apresentar o código em Python. Se você não tem o Python instalado, consulte um guia de instalação ou utilize um compilador online.
def insertion_sort(arr, n):
for i in range(1, n):
## posição e elemento atuais
current_position = i
current_element = arr[i]
## iterar até
### alcançar o primeiro elemento ou
### o elemento atual ser menor que o anterior
while current_position > 0 and current_element < arr[current_position - 1]:
## atualizando o elemento atual com o anterior
arr[current_position] = arr[current_position - 1]
## movendo para a posição anterior
current_position -= 1
## atualizando o elemento da posição atual
arr[current_position] = current_element
if __name__ == '__main__':
## inicialização do array
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
## impressão do array
print(str(arr))
Ordenação por Seleção: Encontrando o Mínimo
A ordenação por seleção possui uma semelhança com a ordenação por inserção, mas com uma diferença crucial. Assim como o algoritmo anterior, este também divide o array em partes ordenadas e não ordenadas. A cada iteração, ele identifica o menor elemento na parte não ordenada e o coloca na última posição da parte ordenada.
Para melhor entendimento, acompanhe a ilustração visual do processo de ordenação por seleção:
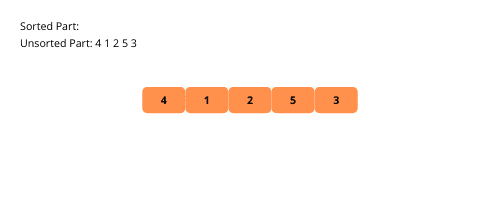
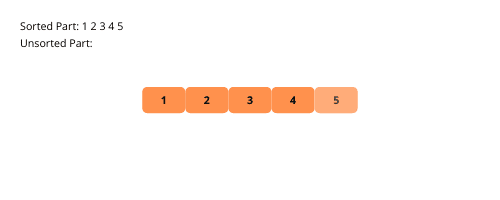
Vejamos os passos para implementar a ordenação por seleção:
- Inicialize o array com dados fictícios (inteiros).
- Percorra o array.
- Mantenha o índice do elemento mínimo.
- Inicie um loop que percorre do elemento atual até o último elemento.
- Verifique se o elemento atual é menor que o elemento mínimo.
- Se o elemento atual for menor que o mínimo, atualize o índice do mínimo.
- Troque o elemento atual pelo elemento mínimo usando os índices.
A complexidade de tempo da ordenação por seleção é O(n²), e a complexidade de espaço é O(1).
Com a explicação detalhada, você pode implementar esse algoritmo com facilidade. Abaixo, você encontra o código de referência:
def selection_sort(arr, n):
for i in range(n):
## para armazenar o índice do elemento mínimo
min_element_index = i
for j in range(i + 1, n):
## verificando e substituindo o índice do elemento mínimo
if arr[j] < arr[min_element_index]:
min_element_index = j
## trocando o elemento atual com o elemento mínimo
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
## inicialização do array
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
## impressão do array
print(str(arr))
Ordenação por Bolha: Trocas Adjacentes
O algoritmo de ordenação por bolha, também conhecido como bubble sort, é um método de ordenação simples. Ele realiza trocas de elementos adjacentes em cada iteração até que o array esteja totalmente ordenado.
O algoritmo itera sobre o array, comparando elementos adjacentes e movendo o elemento atual para a próxima posição se ele for maior que o elemento seguinte.
Para facilitar o entendimento, acompanhe as ilustrações do processo de ordenação por bolha:
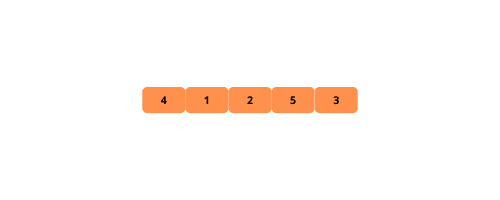
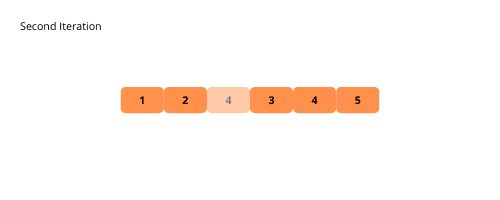
Vejamos os passos para implementar o bubble sort:
- Inicialize o array com dados fictícios (inteiros).
- Percorra o array.
- Itere de 0 até n-i-1. Os últimos “i” elementos já estão ordenados.
- Compare o elemento atual com o próximo elemento.
- Se o elemento atual for maior que o próximo, troque os dois elementos.
A complexidade de tempo do bubble sort é O(n²), enquanto sua complexidade de espaço é O(1).
Com as informações detalhadas, você já pode implementar o bubble sort. O código de referência está abaixo:
def bubble_sort(arr, n):
for i in range(n):
## iterando de 0 até n-i-1, pois os últimos i elementos já estão ordenados
for j in range(n - i - 1):
## verificando o próximo elemento
if arr[j] > arr[j + 1]:
## trocando elementos adjacentes
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
## inicialização do array
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
## imprimindo o array
print(str(arr))
Ordenação por Intercalação: Dividir e Conquistar
A ordenação por intercalação (merge sort) é um algoritmo recursivo que utiliza a estratégia de “dividir e conquistar” para ordenar um array. Em termos de complexidade de tempo, este método é mais eficiente que os algoritmos anteriores.
O merge sort divide o array em duas metades, ordena cada metade recursivamente e, em seguida, intercala as duas metades ordenadas em um único array ordenado. Esse processo de divisão continua até que cada sub-array contenha apenas um elemento, que é considerado ordenado.
Para facilitar a compreensão, acompanhe a ilustração visual do processo de ordenação por intercalação:
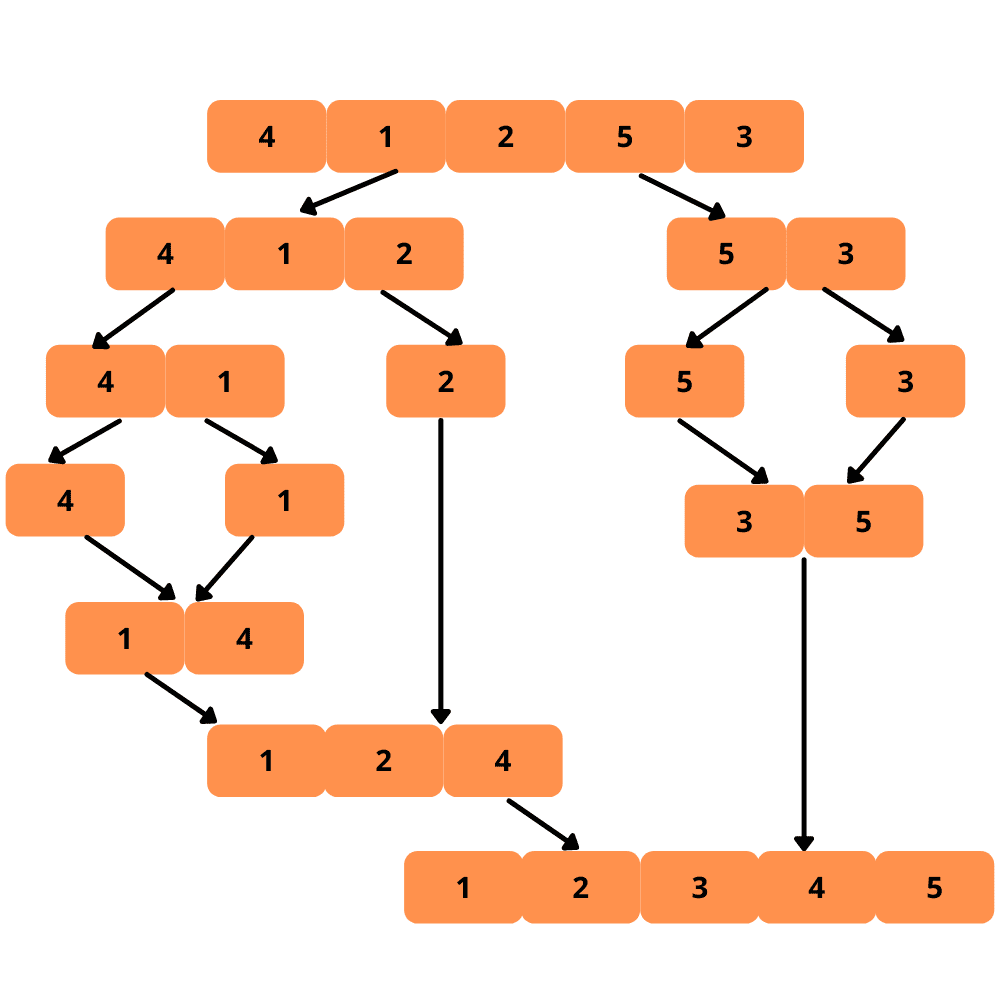
Vejamos os passos para implementar o merge sort:
- Inicialize o array com dados fictícios (inteiros).
- Crie uma função chamada ‘merge’ que intercala dois sub-arrays em um único array ordenado. Essa função recebe como argumentos o array, o índice esquerdo, o índice do meio e o índice direito.
- Calcule os comprimentos dos sub-arrays esquerdo e direito a partir dos índices.
- Copie os elementos do array para os sub-arrays esquerdo e direito.
- Percorra os dois sub-arrays.
- Compare os elementos dos dois sub-arrays.
- Substitua o elemento no array pelo menor elemento dos dois sub-arrays.
- Verifique se restam elementos em algum dos sub-arrays.
- Adicione-os ao array.
- Crie uma função chamada ‘merge_sort’ que recebe como argumentos o array, o índice esquerdo e o índice direito.
- Se o índice esquerdo for maior ou igual ao índice direito, retorne.
- Calcule o ponto médio do array para dividi-lo em duas metades.
- Chame recursivamente a função ‘merge_sort’ para cada metade.
- Após as chamadas recursivas, intercale o array utilizando a função ‘merge’.
A complexidade de tempo do merge sort é O(n log n), e sua complexidade de espaço é O(n).
Com esta explicação, você já pode implementar o merge sort. O código de referência está abaixo:
def merge(arr, left_index, mid_index, right_index):
## sub-arrays esquerdo e direito
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
## obtendo os comprimentos dos sub-arrays
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
## índices para intercalar dois arrays
i = j = 0
## índice para substituição dos elementos no array
k = left_index
## iterando sobre os dois sub-arrays
while i < left_array_length and j < right_array_length:
## comparando elementos dos arrays esquerdo e direito
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
## adicionando os elementos restantes dos arrays esquerdo e direito
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
## caso base para a função recursiva
if left_index >= right_index:
return
## encontrando o índice médio
mid_index = (left_index + right_index) // 2
## chamadas recursivas
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
## intercalando os dois sub-arrays
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
## inicialização do array
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
## impressão do array
print(str(arr))
Conclusão
Este artigo apresentou alguns dos algoritmos de ordenação mais utilizados na programação. Apesar de existirem outros métodos, os abordados aqui são suficientes para o entendimento das principais técnicas de ordenação. Espero que esta exploração tenha sido proveitosa e que tenha despertado seu interesse pelo assunto.
O próximo passo é explorar os algoritmos de busca, que são complementares aos algoritmos de ordenação.
Bons estudos e boa codificação! 👨💻