A Análise Big O é uma metodologia empregada para avaliar e categorizar a eficiência de algoritmos, permitindo a seleção dos mais eficazes e escaláveis. Este guia prático sobre Big O aborda tudo o que é necessário saber sobre essa notação.
O que é a Análise Big O?
A Análise Big O é uma técnica que examina o comportamento de algoritmos em relação ao aumento do volume de dados de entrada. O foco principal é determinar quão eficientemente um algoritmo opera à medida que a quantidade de dados processados cresce.
Eficiência, neste contexto, refere-se à maneira como os recursos do sistema são utilizados durante a execução de um algoritmo para produzir um resultado. Os recursos mais críticos são tempo de processamento e consumo de memória.
Assim, ao aplicar a Análise Big O, as questões centrais são:
- Como o uso de memória de um algoritmo se altera conforme o tamanho dos dados de entrada aumenta?
- Como o tempo necessário para um algoritmo gerar um resultado se modifica com o crescimento do volume de dados de entrada?
A resposta à primeira pergunta define a complexidade espacial do algoritmo, enquanto a segunda define a complexidade temporal. Utilizamos a Notação Big O para expressar as respostas a estas questões. Detalhes sobre isso serão abordados adiante neste guia.
Pré-requisitos
É importante notar que, para aproveitar ao máximo este guia sobre Big O, é necessário ter um conhecimento básico de álgebra. Além disso, como os exemplos serão em Python, alguma familiaridade com essa linguagem também será útil. No entanto, não é necessário um conhecimento avançado, pois não será preciso escrever nenhum código.
Como Realizar a Análise Big O
Nesta seção, vamos explorar como aplicar a Análise Big O.
Ao efetuar a Análise de Complexidade Big O, é crucial ter em mente que o desempenho de um algoritmo depende da forma como os dados de entrada estão organizados.
Por exemplo, algoritmos de ordenação costumam ter um desempenho mais rápido quando os dados já estão em ordem. Este é o melhor cenário possível. Por outro lado, esses mesmos algoritmos podem ser muito mais lentos se os dados estiverem dispostos na ordem inversa. Este seria o pior cenário.
Na Análise Big O, consideramos sempre o pior cenário possível.
Análise de Complexidade Espacial
Iniciamos este guia de Big O examinando como realizar análises de complexidade espacial. O objetivo é observar como a necessidade de memória adicional de um algoritmo varia conforme a quantidade de dados de entrada aumenta.
Por exemplo, a função abaixo utiliza recursão para fazer um loop de `n` até zero. Sua complexidade espacial é diretamente proporcional a `n`. Isso acontece porque, conforme `n` cresce, o número de chamadas à função na pilha de execução também aumenta, resultando em uma complexidade espacial de O(n).
def loop_recursivamente(n):
if n == -1:
return
else:
print(n)
loop_recursivamente(n - 1)
Uma implementação mais eficiente seria:
def loop_normalmente(n):
contador = n
while contador >= 0:
print(contador)
contador =- 1
Nesse segundo algoritmo, apenas uma variável adicional é criada, e ela é utilizada para controlar o loop. Mesmo se `n` aumentasse significativamente, o uso de apenas uma variável adicional persistiria. Portanto, o algoritmo possui uma complexidade espacial constante, denotada por “O(1)”.
Ao comparar a complexidade espacial dos dois algoritmos, concluímos que o loop `while` é mais eficiente que a recursão. Este é o propósito da Análise Big O: avaliar como algoritmos se comportam ao lidar com conjuntos de dados de entrada maiores.
Análise de Complexidade Temporal

Ao realizar a análise de complexidade temporal, não estamos focados no tempo total de execução, mas sim no crescimento do número de operações computacionais executadas. Isso ocorre porque o tempo real de execução pode ser afetado por diversos fatores de sistema, difíceis de quantificar. Assim, rastreamos apenas como o número de operações computacionais cresce, assumindo que cada operação tem um custo semelhante.
Para ilustrar a análise de complexidade temporal, considere o exemplo abaixo:
Imagine que temos uma lista de usuários, cada um com um ID e um nome. O objetivo é criar uma função que retorne o nome do usuário ao receber seu ID. Veja como isso pode ser implementado:
usuarios = [
{'id': 0, 'nome': 'Alice'},
{'id': 1, 'nome': 'Bob'},
{'id': 2, 'nome': 'Charlie'},
]
def obter_nome_usuario(id, usuarios):
for usuario in usuarios:
if usuario['id'] == id:
return usuario['nome']
return 'Usuário não encontrado'
obter_nome_usuario(1, usuarios)
Com base na lista de usuários, o algoritmo itera por toda a lista para encontrar o usuário com o ID correspondente. Se houver 3 usuários, 3 iterações serão executadas. Se houver 10, serão 10 iterações.
Portanto, o número de operações cresce linearmente e é diretamente proporcional ao número de usuários. Nesse caso, o algoritmo tem uma complexidade temporal linear. No entanto, o algoritmo pode ser melhorado.
Suponha que, em vez de armazenar usuários em uma lista, os armazenemos em um dicionário. A função para encontrar o usuário seria:
usuarios = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def obter_nome_usuario(id, usuarios):
if id in usuarios:
return usuarios[id]
else:
return 'Usuário não encontrado'
obter_nome_usuario(1, usuarios)
Com esse novo algoritmo, seja qual for o número de usuários no dicionário, o número de operações necessárias para encontrar o nome do usuário é constante. Ou seja, à medida que o número de usuários aumenta, o número de operações computacionais permanece o mesmo.
Portanto, esse novo algoritmo tem complexidade constante. O número de operações computacionais é invariável, independentemente do número de usuários.
O que é a Notação Big O?
Na seção anterior, discutimos como calcular as complexidades espacial e temporal Big O de diferentes algoritmos. Usamos termos como “linear” e “constante” para descrever essas complexidades. Uma forma mais precisa de descrever essas complexidades é através da Notação Big O.
A Notação Big O é uma maneira de expressar as complexidades de espaço ou tempo de um algoritmo. A notação é relativamente simples: é representada por um “O” seguido de parênteses. Dentro dos parênteses, escrevemos uma função de `n` para representar a complexidade específica.
A complexidade linear é representada por `n`, e é escrita como O(n) (lê-se “O de n”). A complexidade constante é representada por `1`, e escrita como O(1).
Existem outras complexidades, que serão discutidas na próxima seção. Para determinar a complexidade de um algoritmo, geralmente seguimos os seguintes passos:
- Desenvolvemos uma função matemática de `n`, `f(n)`, onde `f(n)` representa o uso de espaço ou o número de operações computacionais executadas pelo algoritmo, e `n` é o tamanho da entrada.
- Identificamos o termo mais dominante nessa função. A ordem de dominância dos termos, do mais para o menos dominante, é: Fatorial, Exponencial, Polinomial, Quadrática, Linearítmica, Linear, Logarítmica e Constante.
- Eliminamos quaisquer coeficientes do termo.
O resultado desse processo se torna o termo que utilizamos dentro dos parênteses.
Exemplo:
Considere a seguinte função em Python:
usuarios = [
'Alice',
'Bob',
'Charlie'
]
def imprimir_usuarios(usuarios):
numero_de_usuarios = len(usuarios)
print("Número total de usuários:", numero_de_usuarios)
for i in range(numero_de_usuarios):
print(i, end=': ')
print(usuarios[i])
Agora, calcularemos a complexidade temporal Big O desse algoritmo.
Primeiro, construímos uma função matemática de `n`, `f(n)`, para representar o número de operações computacionais executadas pelo algoritmo. Lembre-se de que `n` representa o tamanho da entrada.
No código, a função realiza duas operações iniciais: uma para calcular o número de usuários e outra para exibir esse número. Depois, para cada usuário, executa mais duas operações: uma para imprimir o índice e outra para imprimir o nome.
A função que melhor representa o número de operações computacionais pode ser escrita como `f(n) = 2 + 2n`, onde `n` é o número de usuários.
Na segunda etapa, selecionamos o termo mais dominante. `2n` é um termo linear, e `2` é um termo constante. Linear é mais dominante do que constante, então escolhemos `2n` como termo dominante.
Assim, a função se torna `f(n) = 2n`.
A última etapa é eliminar os coeficientes. Em nossa função, `2` é o coeficiente. Eliminando-o, a função se torna `f(n) = n`. Este é o termo que usamos dentro dos parênteses.
Portanto, a complexidade temporal do nosso algoritmo é O(n), ou complexidade linear.
Diferentes Complexidades Big O
A última seção deste guia apresentará as diferentes complexidades e os gráficos correspondentes.
#1. Constante

Complexidade constante indica que o algoritmo usa uma quantidade fixa de memória (na análise de complexidade espacial) ou executa um número constante de operações (na análise de complexidade temporal). Essa é a complexidade ideal, pois o algoritmo não requer recursos adicionais conforme o tamanho da entrada aumenta, o que o torna altamente escalável.
A complexidade constante é representada como O(1). No entanto, nem sempre é possível criar algoritmos com complexidade constante.
#2. Logarítmico
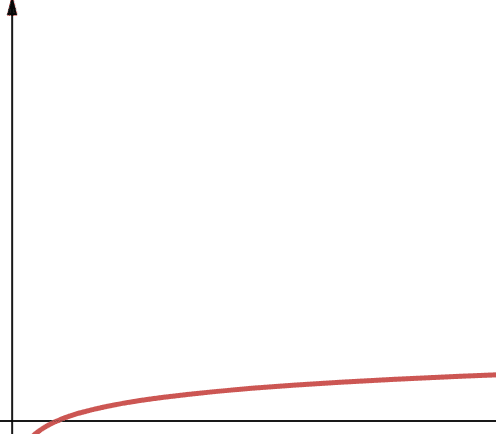
A complexidade logarítmica é expressa como O(log n). É importante observar que, em Ciência da Computação, se a base do logaritmo não for especificada, assumimos que ela é 2.
Portanto, `log n` é `log2n`. Funções logarítmicas crescem rapidamente no início e depois diminuem. Isso significa que elas escalam bem e trabalham de forma eficiente com números cada vez maiores de `n`.
#3. Linear
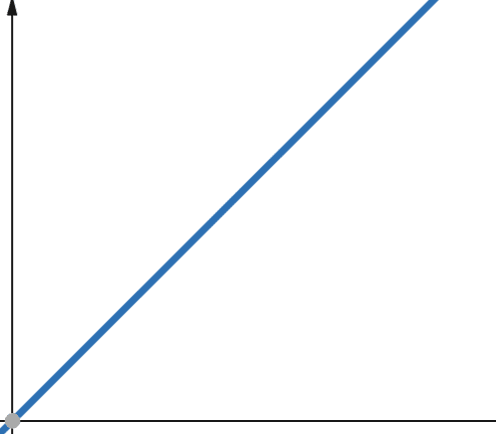
Em funções lineares, se a variável independente é multiplicada por um fator `p`, a variável dependente é multiplicada pelo mesmo fator `p`.
Assim, uma função com complexidade linear cresce na mesma proporção que o tamanho da entrada. Se o tamanho da entrada dobrar, o mesmo acontecerá com o número de operações computacionais ou com o uso de memória. A complexidade linear é representada por O(n).
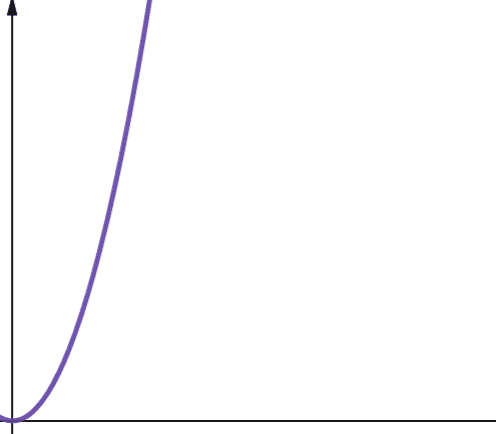
#4. Linearítmico
O(n * log n) representa funções linearítmicas. Essas funções são o resultado da multiplicação de uma função linear por uma função logarítmica. Elas produzem resultados ligeiramente maiores que as funções lineares quando `log n` é maior que 1. Isso ocorre porque `n` aumenta ao ser multiplicado por um número maior que 1.
`Log n` é maior que 1 para todos os valores de `n` maiores que 2 (lembrando que `log n` é `log2n`). Portanto, para valores de `n` maiores que 2, as funções linearítmicas são menos escaláveis que as lineares. Na maioria dos casos, `n` é maior que 2. Por isso, as funções linearítmicas são geralmente menos escaláveis que as logarítmicas.
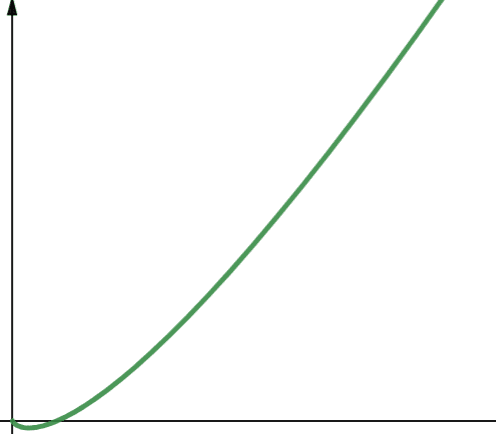
#5. Quadrático
A complexidade quadrática é representada por O(n²). Isso significa que se o tamanho da entrada aumentar 10 vezes, o número de operações executadas ou o espaço utilizado aumentará 10² vezes, ou seja, 100 vezes. Isso não é muito escalável e, como pode ser observado no gráfico, a complexidade cresce rapidamente.
A complexidade quadrática surge em algoritmos onde um loop é executado `n` vezes e, para cada iteração, outro loop é executado `n` vezes novamente, como no algoritmo Bubble Sort. Embora geralmente não seja o ideal, às vezes não há alternativa a não ser implementar algoritmos com complexidade quadrática.
#6. Polinomial
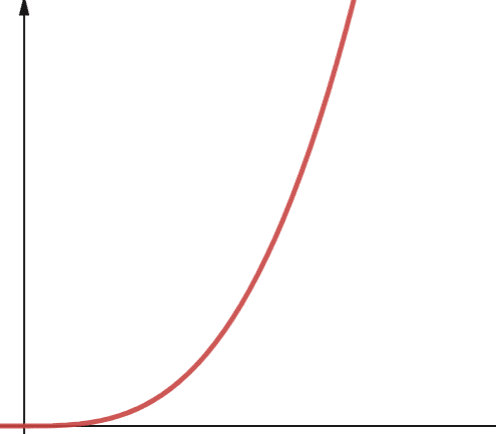
Um algoritmo com complexidade polinomial é representado por O(n^p), onde `p` é um número inteiro constante. `p` representa a ordem em que `n` é elevado.
Essa complexidade surge quando temos um número específico de loops aninhados. A diferença entre a complexidade polinomial e a quadrática é que a quadrática é da ordem de 2, enquanto a polinomial pode ter qualquer número inteiro maior que 2.
#7. Exponencial
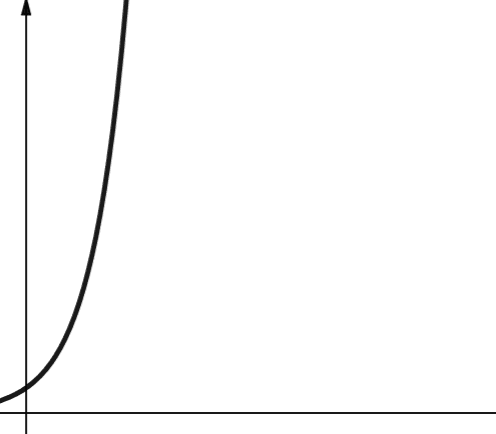
A complexidade exponencial cresce ainda mais rápido que a complexidade polinomial. Em matemática, o valor padrão para uma função exponencial é a constante `e` (número de Euler). Em Ciência da Computação, o valor padrão para uma função exponencial é 2.
A complexidade exponencial é representada por O(2^n). Quando `n` é 0, 2^n é 1. Mas quando `n` aumenta para 5, 2^n aumenta para 32. Um aumento de `n` em uma unidade dobra o valor anterior. Portanto, funções exponenciais não são muito escaláveis.
#8. Fatorial
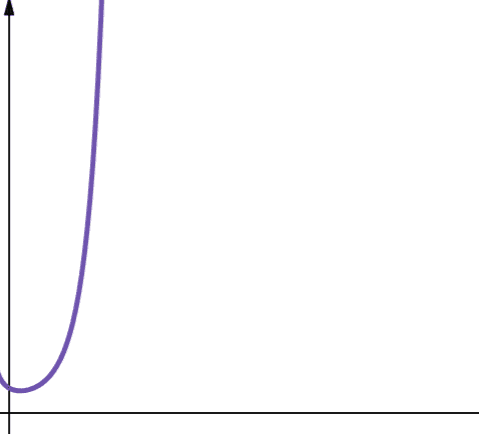
A complexidade fatorial é representada por O(n!). Essa função também cresce muito rapidamente e, portanto, não é escalável.
Conclusão
Este artigo abordou a Análise Big O e como calculá-la. Também discutimos as diferentes complexidades e sua escalabilidade.
A seguir, você pode praticar a análise Big O em algoritmos de ordenação em Python.