O algoritmo de Máquina de Vetores de Suporte (SVM) destaca-se como um dos métodos mais populares no campo do aprendizado de máquina. Sua eficácia e capacidade de treinamento com conjuntos de dados limitados o tornam uma ferramenta valiosa. Mas afinal, o que é exatamente uma SVM?
O que Define uma Máquina de Vetores de Suporte (SVM)?
Uma Máquina de Vetores de Suporte é um tipo de algoritmo de aprendizado de máquina que utiliza o aprendizado supervisionado para construir modelos de classificação binária. Essa definição pode parecer complexa, mas este artigo irá desmistificar o SVM e explorar sua relação com o processamento de linguagem natural. Primeiramente, vamos entender o funcionamento interno de uma máquina de vetores de suporte.
Como a SVM Opera?
Imagine um problema de classificação simples, onde temos dados com duas características, denominadas x e y, e uma saída correspondente, que pode ser categorizada como vermelha ou azul. Podemos representar visualmente esses dados em um gráfico:
Diante desses dados, o objetivo é estabelecer um limite de decisão. Esse limite é uma linha que separa as duas categorias de pontos de dados. Observando o mesmo conjunto de dados, mas com um limite de decisão definido:
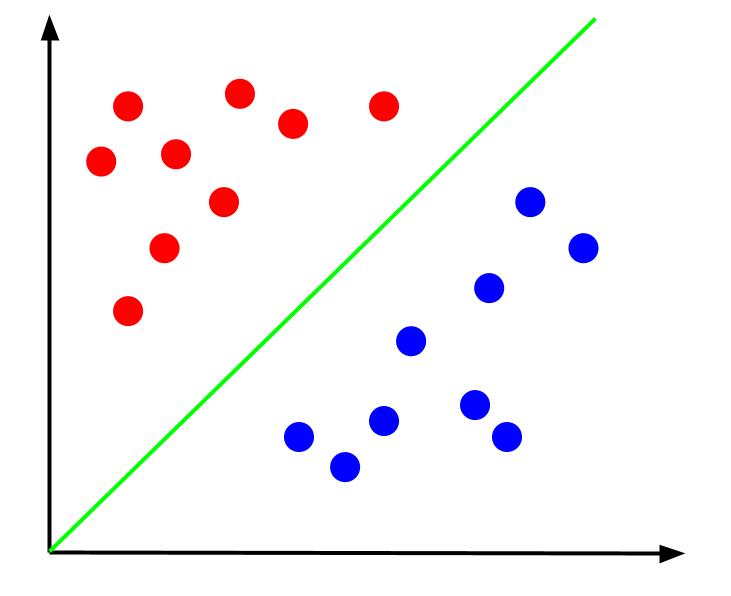
Com esse limite de decisão, podemos prever a qual categoria um ponto de dados pertence, com base em sua localização em relação a esse limite. O algoritmo de Máquina de Vetores de Suporte é responsável por criar o limite de decisão ideal para classificar os pontos.
Mas, o que realmente significa um “melhor” limite de decisão?
Um argumento válido é que o melhor limite de decisão é aquele que maximiza a distância em relação a qualquer um dos vetores de suporte. Os vetores de suporte são pontos de dados de ambas as classes que estão mais próximos da classe oposta, representando o maior risco de classificação incorreta devido à sua proximidade.
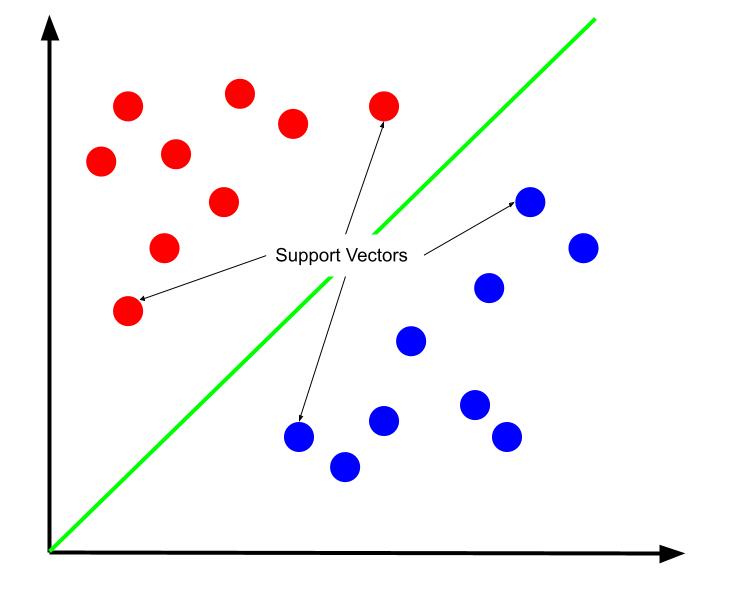
Assim, o processo de treinamento de uma máquina de vetores de suporte envolve a busca por uma linha que amplie a margem entre os vetores de suporte.
É crucial destacar que, como o limite de decisão é posicionado com base nos vetores de suporte, eles são os únicos determinantes da posição desse limite. Os demais pontos de dados tornam-se, portanto, redundantes. Dessa forma, o treinamento requer apenas o uso dos vetores de suporte.
Neste exemplo, o limite de decisão é uma linha reta, o que ocorre porque o conjunto de dados tem apenas duas características. Quando o conjunto de dados possui três características, o limite de decisão toma a forma de um plano. E quando há quatro ou mais características, o limite de decisão é denominado hiperplano.
Dados Não Linearmente Separados
O exemplo anterior abordou dados simples que podem ser separados por um limite de decisão linear. Considere agora um cenário diferente, onde os dados são representados da seguinte forma:
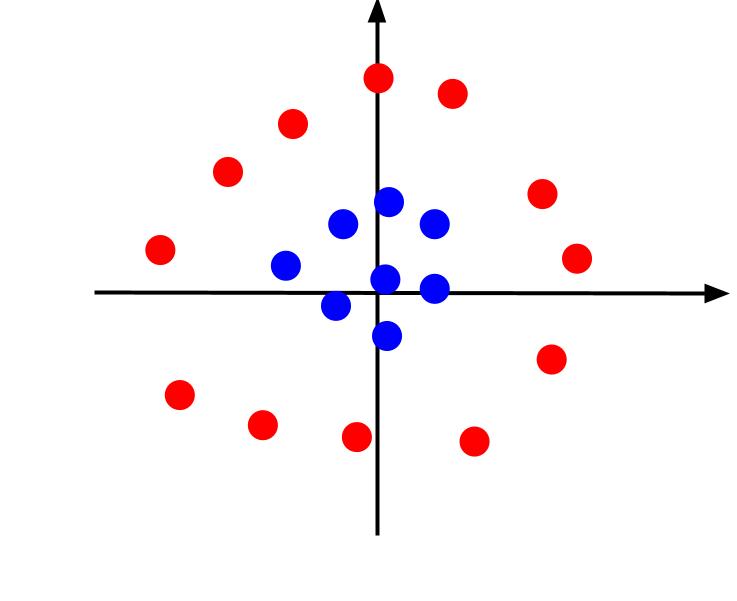
Nesta situação, é impossível separar os dados com uma linha. No entanto, podemos introduzir uma terceira característica, denominada z, definida pela equação: z = x² + y². Ao adicionar z como um terceiro eixo, transformamos o plano em um espaço tridimensional.
Ao visualizar o gráfico 3D de um ângulo onde o eixo x é horizontal e o eixo z é vertical, temos uma perspectiva semelhante a esta:
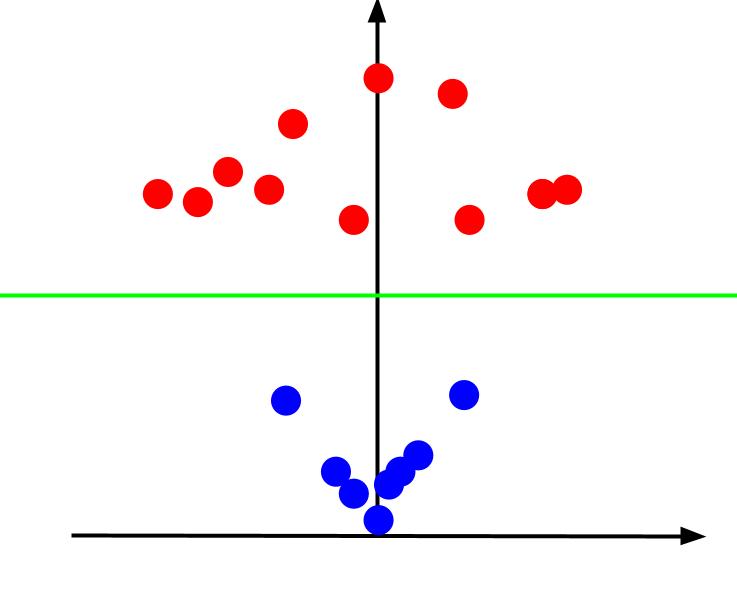
O valor z representa a distância de um ponto à origem em relação aos outros pontos no plano XY original. Assim, os pontos azuis mais próximos da origem têm valores z menores.
Enquanto isso, os pontos vermelhos mais distantes da origem possuem valores z maiores. Ao plotar os pontos em relação aos seus valores z, obtemos uma separação clara que pode ser demarcada por um limite de decisão linear, como ilustrado.
Essa é uma ideia poderosa utilizada em Máquinas de Vetores de Suporte. Em termos gerais, trata-se de mapear os dados em dimensões superiores para que os pontos possam ser separados por um limite linear. As funções responsáveis por esse processo são conhecidas como funções kernel, e existem diversas opções, incluindo sigmoide, linear, não linear e RBF.
Para tornar o mapeamento dessas características mais eficiente, a SVM utiliza um truque do kernel.
SVM no Aprendizado de Máquina
A Máquina de Vetores de Suporte é um dos muitos algoritmos utilizados no aprendizado de máquina, ao lado de outras opções populares, como Árvores de Decisão e Redes Neurais. É valorizada por sua capacidade de funcionar bem com menos dados em comparação com outros algoritmos. As SVMs são comumente usadas para:
- Classificação de texto: categorização de dados textuais, como comentários e avaliações, em uma ou mais classes.
- Detecção facial: análise de imagens para identificar rostos, sendo útil em aplicações como filtros de realidade aumentada.
- Classificação de imagens: as SVMs podem classificar imagens de forma eficaz, superando outras abordagens.
O Desafio da Classificação de Texto
A internet está repleta de grandes volumes de dados textuais, muitos dos quais não são estruturados ou rotulados. Para melhor aproveitar e compreender esses dados textuais, a classificação se torna essencial. Exemplos de situações onde a classificação de texto é usada incluem:
- Categorização de tweets em tópicos para que os usuários possam seguir assuntos de interesse.
- Classificação de e-mails em categorias como Social, Promoções ou Spam.
- Classificação de comentários em fóruns públicos como ofensivos ou não.
Como a SVM Funciona na Classificação de Linguagem Natural
A Máquina de Vetores de Suporte é usada para classificar textos entre aqueles que pertencem a um tópico específico e aqueles que não pertencem. Isso é alcançado convertendo e representando os dados textuais em um conjunto de dados com várias características.
Uma maneira de fazer isso é criar características para cada palavra no conjunto de dados. Para cada ponto de dados de texto, registramos o número de ocorrências de cada palavra. Se houver palavras únicas no conjunto de dados, teremos características no conjunto de dados.
Além disso, fornecemos classificações para esses pontos de dados. Embora as classificações sejam rotuladas por texto, a maioria das implementações de SVM espera rótulos numéricos.
Portanto, os rótulos precisam ser convertidos em números antes do treinamento. Após a preparação do conjunto de dados, usando essas características como coordenadas, podemos usar um modelo SVM para classificar o texto.
Criando uma SVM em Python
Para construir uma Máquina de Vetores de Suporte (SVM) em Python, podemos usar a classe SVC da biblioteca sklearn.svm. Aqui está um exemplo de como usar a classe SVC para criar um modelo SVM em Python:
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
# Carregar o conjunto de dados
X = ...
y = ...
# Dividir os dados em conjuntos de treinamento e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
# Criar um modelo SVM
model = SVC(kernel="linear")
# Treinar o modelo com os dados de treinamento
model.fit(X_train, y_train)
# Avaliar o modelo nos dados de teste
accuracy = model.score(X_test, y_test)
print("Precisão: ", accuracy)
Neste exemplo, importamos primeiro a classe SVC da biblioteca sklearn.svm. Em seguida, carregamos o conjunto de dados e o dividimos em conjuntos de treinamento e teste.
Criamos um modelo SVM instanciando um objeto SVC e especificando o parâmetro do kernel como ‘linear’. Em seguida, treinamos o modelo com os dados de treinamento usando o método fit e avaliamos o modelo com os dados de teste usando o método score. O método score retorna a precisão do modelo, que é exibida no console.
Também é possível especificar outros parâmetros para o objeto SVC, como o parâmetro C, que controla a intensidade da regularização, e o parâmetro gama, que define o coeficiente do kernel para determinados kernels.
Vantagens da SVM
Aqui estão algumas vantagens do uso de Máquinas de Vetores de Suporte (SVMs):
- Eficiência: SVMs geralmente são eficientes no treinamento, especialmente com conjuntos de dados grandes.
- Resistência ao ruído: SVMs são relativamente resistentes ao ruído nos dados de treinamento, pois procuram o classificador de margem máxima, o qual é menos sensível ao ruído do que outros classificadores.
- Eficiência de memória: SVMs exigem apenas um subconjunto dos dados de treinamento na memória em qualquer momento, tornando-os mais eficientes em termos de memória do que outros algoritmos.
- Desempenho em espaços de alta dimensão: SVMs podem ter um bom desempenho mesmo quando o número de características é maior do que o número de amostras.
- Versatilidade: SVMs podem ser usadas para tarefas de classificação e regressão, e podem lidar com diferentes tipos de dados, incluindo dados lineares e não lineares.
A seguir, vamos explorar alguns recursos para aprofundar o conhecimento em Máquinas de Vetores de Suporte (SVM).
Recursos de Aprendizado
Uma Introdução às Máquinas de Vetores de Suporte
O livro “Introdução às Máquinas de Vetores de Suporte” oferece uma visão abrangente e gradual dos métodos de aprendizado baseados em kernel.
Ele proporciona uma base sólida na teoria das máquinas de vetores de suporte.
Aplicações de Máquinas de Vetores de Suporte
Enquanto o livro anterior foca na teoria das SVMs, o livro “Aplicações de Máquinas de Vetores de Suporte” destaca suas aplicações práticas.
Ele examina como as SVMs são usadas no processamento de imagens, reconhecimento de padrões e visão computacional.
Máquinas de Vetores de Suporte (Ciência da Informação e Estatística)
O objetivo do livro “Máquinas de Vetores de Suporte (Ciência da Informação e Estatística)” é fornecer uma visão geral dos princípios por trás da eficácia das SVMs em diversas aplicações.
Os autores enfatizam vários fatores que contribuem para o sucesso das SVMs, incluindo sua capacidade de operar bem com um número limitado de parâmetros ajustáveis, sua resistência a vários tipos de erros e anomalias e seu desempenho computacional eficiente em comparação com outros métodos.
Aprendendo com Kernels
“Aprendendo com Kernels” é um livro que introduz os leitores às máquinas de vetores de suporte (SVMs) e às técnicas de kernel relacionadas.
O livro é projetado para fornecer aos leitores uma compreensão básica da matemática e o conhecimento necessário para começar a usar algoritmos de kernel no aprendizado de máquina. O objetivo é oferecer uma introdução completa, mas acessível, às SVMs e aos métodos de kernel.
Máquinas de Vetores de Suporte com Sci-kit Learn
O curso online “Máquinas de Vetores de Suporte com Sci-kit Learn” da rede de projetos Coursera ensina como implementar um modelo SVM usando a popular biblioteca de aprendizado de máquina Sci-Kit Learn.

Além disso, o curso aborda a teoria por trás das SVMs, além de seus pontos fortes e limitações. O curso é de nível iniciante e tem duração de cerca de 2,5 horas.
Máquinas de Vetores de Suporte em Python: Conceitos e Código
O curso online pago “Máquinas de Vetores de Suporte em Python” da Udemy tem até 6 horas de instrução em vídeo e oferece um certificado.

Ele cobre as SVMs e como elas podem ser implementadas de maneira sólida em Python. O curso também aborda as aplicações de negócios das Máquinas de Vetores de Suporte.
Aprendizado de Máquina e IA: Máquinas de Vetores de Suporte em Python
Neste curso sobre Aprendizado de Máquina e IA, você aprenderá a usar as máquinas de vetores de suporte (SVMs) para várias aplicações práticas, incluindo reconhecimento de imagem, detecção de spam, diagnóstico médico e análise de regressão.

Você utilizará a linguagem de programação Python para implementar modelos de ML para essas aplicações.
Considerações Finais
Neste artigo, exploramos brevemente a teoria por trás das Máquinas de Vetores de Suporte, sua aplicação no Aprendizado de Máquina e no Processamento de Linguagem Natural.
Também demonstramos sua implementação usando o scikit-learn. Além disso, discutimos as aplicações práticas e as vantagens das Máquinas de Vetores de Suporte.
Este artigo serviu como uma introdução, e os recursos adicionais recomendados podem fornecer mais detalhes, explicando em profundidade as Máquinas de Vetores de Suporte. Por sua versatilidade e eficiência, o estudo das SVMs é essencial para o crescimento como cientista de dados e engenheiro de ML.
A seguir, você pode explorar os principais modelos de aprendizado de máquina.