Em uma análise de dados, o erro percentual quantifica a disparidade entre os valores precisos e suas estimativas, em relação ao valor original. Esta métrica é expressa como uma porcentagem, obtida multiplicando-se o resultado por 100.
O erro percentual pode ser apresentado tanto como erro absoluto quanto como erro relativo. Vários fatores podem gerar erros, como imprecisões em equipamentos, falhas de cálculo, erros de medição e até condições ambientais adversas.
O erro percentual é essencial para avaliarmos a magnitude dos desvios em nossas análises. Um erro percentual baixo indica uma proximidade do valor original, enquanto erros mais altos revelam uma divergência significativa entre o valor real e o valor aproximado.
Por exemplo, um erro de 2% demonstra que a estimativa está bem próxima do valor verdadeiro, ao passo que um erro de 56% aponta uma grande discrepância entre os valores.
Erros de medição são comuns, seja por instabilidade ao medir, defeitos nos instrumentos, imprecisão dos materiais ou outros fatores.
Cálculo do Erro Percentual
Para determinar o erro percentual, é necessário dispor de dois valores: o valor exato e o valor aproximado. A subtração do valor aproximado do valor exato, seguida pela divisão do resultado pelo valor exato, nos fornece o erro relativo. A multiplicação desse erro relativo por 100 converte-o em erro percentual.
Erro Percentual = [(Valor Exato – Valor Estimado) / Valor Exato] × 100
Componentes da Fórmula
Valor Exato: Representa o valor numérico preciso de uma leitura. Idealmente, este deveria ser o valor obtido, mas devido a erros, geralmente não é o que se registra. É o padrão de referência para cálculos.
Valor Estimado: Refere-se ao valor registrado durante uma experiência ou medição. Frequentemente, este valor difere do valor exato por conta de fatores como falhas em equipamentos, erros de leitura ou condições ambientais inadequadas, como correntes de ar ou instrumentos defeituosos.
Exemplos Práticos
Exemplo 1
Um estudante, ao medir a área de um triângulo, obteve o resultado de 462 cm². Entretanto, a área correta do triângulo é de 465 cm². Vamos calcular o erro percentual.
Solução:
Área medida: 462 cm²
Área real: 465 cm²
Cálculo:
Diferença entre o valor real e o valor medido: 465 – 462 = 3 cm² (Este é o erro absoluto).
Divisão do erro pelo valor real: 3 / 465 = 0,00645
Multiplicação do resultado por 100: 0,00645 × 100 = 0,64%
Portanto, o erro percentual no cálculo da área do triângulo é de 0,64%.
Exemplo 2
Em um planejamento de festa, estimava-se a presença de 20 pessoas, mas apenas 18 compareceram. Calcule o erro percentual desta estimativa.
Solução:
Número estimado de pessoas: 20
Número de pessoas presentes: 18
Cálculo:
Diferença entre o valor estimado e o valor final: 20 – 18 = 2 (Este é o erro absoluto).
Divisão do erro pelo valor estimado: 2 / 20 = 0,1
Multiplicação do resultado por 100: 0,1 × 100 = 10%
O erro percentual na estimativa do número de convidados foi de 10%.
Exemplo 3
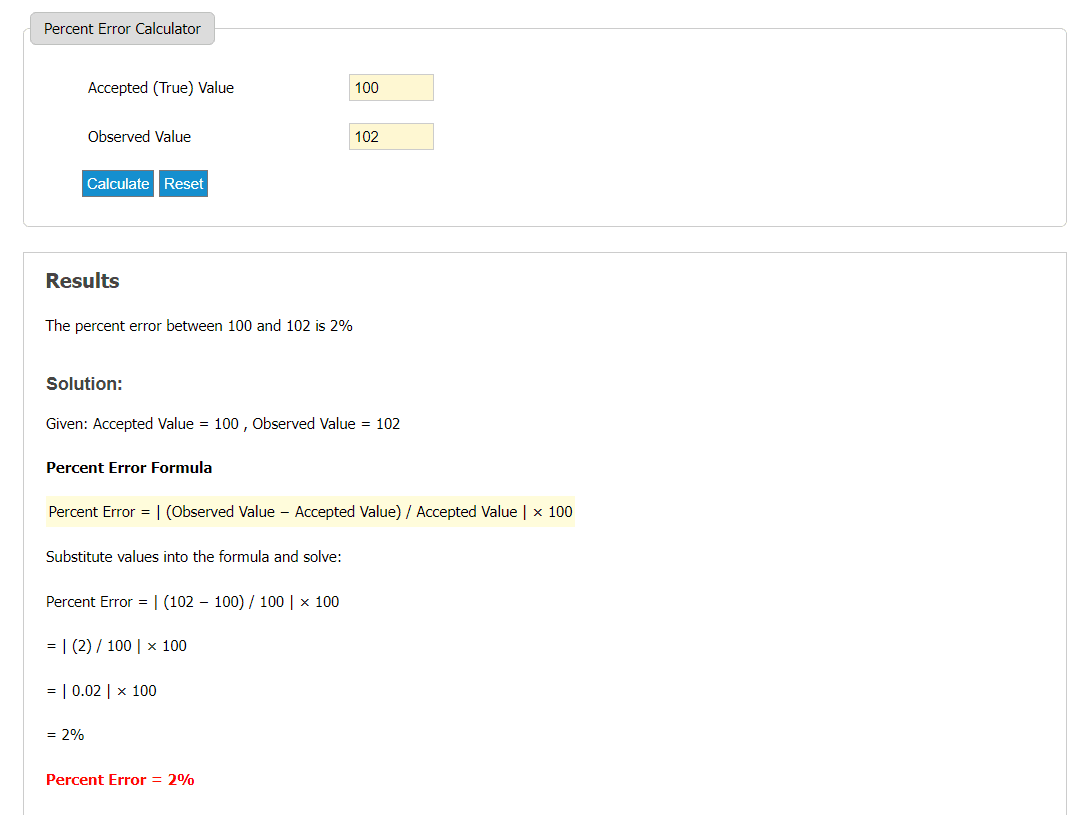
Num experimento para determinar o ponto de ebulição da água, um pesquisador registrou 102°C, enquanto o valor real é 100°C.
Solução:
Ponto de ebulição real da água: 100°C
Ponto de ebulição medido: 102°C
Cálculo:
Diferença entre o valor real e o valor calculado: 100 – 102 = -2°C. Como o erro percentual é um valor absoluto, usamos 2°C.
Divisão do erro pelo valor real: 2 / 100 = 0,02
Multiplicação do resultado por 100: 0,02 × 100 = 2%
Assim, o erro percentual na medição do ponto de ebulição da água é de 2%.
Aplicações do Erro Percentual no Mundo Real
- O erro percentual é crucial para avaliar a precisão de tarefas realizadas, identificando onde ocorreram falhas.
- É uma ferramenta valiosa em laboratórios e indústrias onde a precisão é essencial e não há margem para erros.
- O erro percentual também é útil na produção em massa, garantindo que não haja desvios nos produtos finais.
- Em laboratórios científicos, o uso do erro percentual é imprescindível.
Erro Percentual vs. Erro Absoluto
O erro absoluto é a diferença entre o valor real e o valor medido, mantendo a mesma unidade do valor original.
Exemplo:
Ao pedir 2 kg de mangas, o vendedor pesa 1,98 kg. O erro absoluto é 2 – 1,98 = 0,02 kg.
Por outro lado, o erro percentual é o erro absoluto expresso como porcentagem do valor original, não tendo unidade.
No exemplo anterior, o erro absoluto é 0,02 kg.
Para calcular o erro percentual, dividimos 0,02 por 2 (valor original em kg): 0,02 / 2 = 0,01.
Então, o erro percentual é 0,01 × 100 = 1%.
Erro Percentual vs. Erro Relativo
O erro relativo é a razão entre o erro absoluto e o valor real, indicando o tamanho do erro em relação ao valor verdadeiro.
Exemplo:
A previsão indicava temperatura de 38°C, mas a temperatura chegou a 42°C.
A diferença é: 42°C – 38°C = 4°C.
O erro relativo é: 4 / 38 = 0,1052.
O erro percentual é o erro relativo multiplicado por 100, ou seja, 0,1052 × 100 = 10,52%.
O cálculo do erro percentual, do erro relativo e do erro absoluto pode ser simplificado com calculadoras online, que fornecem os resultados de forma imediata.
Ferramentas para Cálculo de Erros
#1. Calculadora Soup
A Calculadora Soup é útil para determinar o erro percentual entre um valor experimental e um valor real. Basta inserir os valores, e a calculadora fornecerá os resultados automaticamente.
Esta ferramenta exibe duas colunas para os valores, processando automaticamente e retornando os resultados de forma precisa.
#2. Calculator.net
A Calculator.net apresenta duas colunas para inserir valores reais e estimados, permitindo cálculos rápidos e eficientes, especialmente quando há muitos dados a serem analisados.
Esta calculadora simplifica o processo, fornecendo resultados imediatos e precisos.

Erros percentuais são inevitáveis e podem ser minimizados, mas raramente serão zero. Geralmente, chegam a um valor próximo de zero.
#3. Good Calculators
Entre as diversas calculadoras online, a Good Calculators destaca-se pela praticidade. Nela, insere-se o valor estimado e o valor real, e os resultados são fornecidos de forma instantânea.
Essa ferramenta simplifica cálculos extensos, economizando tempo e proporcionando agilidade no processo.
Portanto, as calculadoras são ideais quando se tem muitos dados e pouco tempo para os cálculos.
Conclusão
Erros nos cálculos podem comprometer qualquer projeto ou pesquisa. Para otimizar o trabalho e reduzir erros humanos, as calculadoras online de erro percentual são ferramentas indispensáveis.
Se o seu interesse são finanças, pode consultar calculadoras de percentagem de lucro.