O teste de hipóteses é um método utilizado por muitos analistas nos setores privado e governamental para fazer declarações prováveis ou suposições sobre dados populacionais.
Se você tem lidado ou estudado dados populacionais, deve ter se deparado com esta ferramenta vital de teste de hipóteses.
Muitos métodos podem ser empregados para fazer suposições, mas nem todos fornecem maior precisão.
E se você não tem certeza sobre seus dados, mas ainda deseja usá-los, pode ser arriscado para sua organização.
O teste de hipóteses é uma boa estratégia para atingir um nível mais alto de precisão. Tem sido instrumental na análise da população.
Neste artigo, discutirei o que é o teste de hipóteses, como funciona, seus benefícios e seus casos de uso.
Então, sem mais delongas, vamos começar!
últimas postagens
O que é Teste de Hipóteses?
O teste de hipóteses é um método de inferência estatística que os analistas usam para testar se os dados populacionais disponíveis suportam suficientemente uma determinada hipótese e fazem suposições a partir dela.
Por meio desse método, os analistas podem avaliar facilmente uma hipótese e determinar a precisão da suposição com base nos dados disponíveis.
Em palavras simples, é um processo de teste baseado em estatísticas inferenciais que permite chegar a um veredicto sobre dados populacionais com base em dados de amostra coletados.
Em geral, é quase impossível para os analistas encontrar propriedades ou qualquer parâmetro particular de toda a população. Mas, por meio do teste de hipóteses, você pode fazer uma previsão e uma decisão informadas com base nos dados da amostra e em sua precisão.
Tipos de teste de hipótese
Os diferentes tipos de teste de hipótese são:
- Hipótese Nula: As estatísticas mostram que os dados amostrais são abruptos e não há correlação entre as duas variáveis nos dados amostrais fornecidos.
- Hipótese Alternativa: Demonstra a tese primária e se opõe à hipótese nula. É a principal força motriz no processo de teste porque mostra uma correlação entre duas variáveis nos dados da amostra.
- Hipótese não direcional: esse tipo de teste de hipótese serve como uma hipótese bilateral. Ele mostra que não há direção entre duas variáveis em dados de amostra e que o valor verdadeiro não é o mesmo que o valor previsto.
- Hipótese direcional: A hipótese direcional descreve alguma relação entre duas variáveis. Aqui, uma variável em um dado de amostra pode influenciar as outras variáveis.
- Hipótese estatística: ajuda os analistas a avaliar se os dados e o valor satisfazem uma determinada hipótese. É muito útil para fazer declarações e suposições sobre o resultado de um parâmetro de população de amostra.
Em seguida, vamos discutir métodos de teste de hipóteses.
Métodos de teste de hipóteses
Para avaliar se uma hipótese específica é verdadeira ou não, como analista, você precisará de muitas evidências plausíveis para concluir. Nesse processo de teste, uma hipótese nula e alternativa é estabelecida antes de iniciar a avaliação.
O teste de hipóteses não envolve apenas um único método, mas muitos para avaliar se os dados da amostra são favoráveis. Como analista, você deve considerar os dados e o tamanho da amostra e escolher qual método de teste de hipótese é mais adequado para você.
Teste de normalidade
É um método de teste de hipótese padrão para analisar a distribuição regular em dados de amostra. Durante o processo de teste, é verificado se os pontos de dados agrupados em torno da média estão abaixo ou acima da média.
Neste teste estatístico, a chance de os pontos ficarem acima ou abaixo da média é igualmente provável. Uma curva de sino é formada e é igualmente distribuída em ambos os lados da média.
Teste Z-Test
É outro tipo de teste de hipótese utilizado quando os dados populacionais são normalmente distribuídos. Ele testa se a média de dois parâmetros populacionais separados é diferente quando a variância dos dados é conhecida por você.
Durante a análise de dados populacionais, é muito provável que você utilize esse tipo quando o tamanho da amostra de dados for superior a trinta. Além disso, o teorema do limite central é outro motivo que torna o Z-Test adequado, pois o teorema afirma que quando o tamanho da amostra aumenta, as amostras são normalmente distribuídas.
Teste T-Test
O teste de hipótese do Teste T será usado por você quando o tamanho da amostra for limitado e geralmente distribuído. Em geral, quando o tamanho da amostra está abaixo de 30 e o desvio padrão do parâmetro é desconhecido para você, ele é aplicado principalmente.
Ao fazer um Teste T, você o faz para calcular os intervalos de confiança de dados populacionais específicos.
Teste qui-quadrado
O teste qui-quadrado é um processo popular de teste de hipóteses que é frequentemente usado para avaliar a adequação e a integridade de uma distribuição de dados.
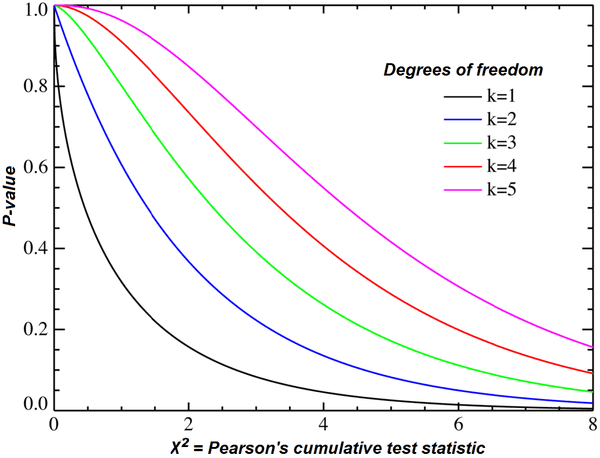Fonte: wikipedia.org
No entanto, o principal motivo pelo qual você utilizará esse tipo de hipótese é quando desejar testar a variação da população em relação a uma variação da população de um valor presumido ou conhecido. Diferentes testes qui-quadrado são realizados, mas o tipo mais comum é o teste qui-quadrado de variância e independência.
Teste ANOVA
Abreviado como Análise de Variância, é um método de teste estatístico que ajuda a comparar os conjuntos de dados de duas amostras. No entanto, permite comparar mais de duas médias de cada vez.
Também explica uma variável dependente e uma variável independente de dados de amostra. O uso de ANOVA é bastante semelhante ao uso de Z-Test e T-Test, mas os dois últimos são limitados a apenas duas médias.
Como funciona o teste de hipóteses?
Todo analista que utiliza o teste de hipóteses utiliza dados de amostra aleatórios para análise e medição. Durante o teste, os dados da amostra aleatória são utilizados para testar a hipótese nula e a hipótese alternativa.
Como discutimos anteriormente, a hipótese nula e a hipótese alternativa são totalmente mutuamente exclusivas e, durante o resultado do teste, apenas uma pode ser verdadeira.
Entretanto, existem alguns casos em que a hipótese nula é rejeitada; a hipótese alternativa nem sempre é verdadeira.
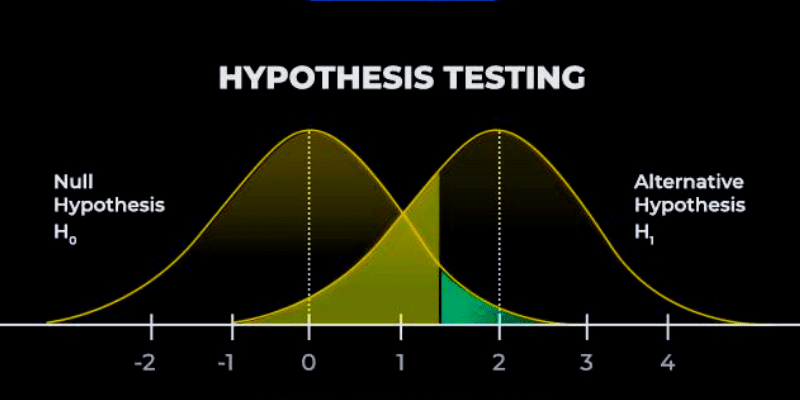Fonte: Etapas do Analytics
Valor-p: Enquanto o processo de teste começa, o valor-p ou valor de probabilidade está envolvido e mostra se o resultado é significativo ou não. Não só isso, mas o p-valor também mostra a probabilidade de ocorrência de erro ao descartar ou não descartar uma hipótese nula durante o teste. O valor-p resultante é 0 ou 1, que é então comparado com o nível de significância ou nível alfa.
O nível de significância aqui define o risco aceitável ao rejeitar uma hipótese nula durante o teste. É importante lembrar que o resultado do teste de hipótese pode levar a dois tipos de erros:
- O erro tipo 1 ocorre quando o resultado do teste descarta a hipótese nula, embora seja verdadeira.
- O erro tipo 2 aparece quando a hipótese nula é aceita pelo resultado da amostra, apesar de ser falsa.
Todos os valores que causam a rejeição da hipótese nula são armazenados na região crítica. E é o valor crítico que separa as regiões críticas das outras.
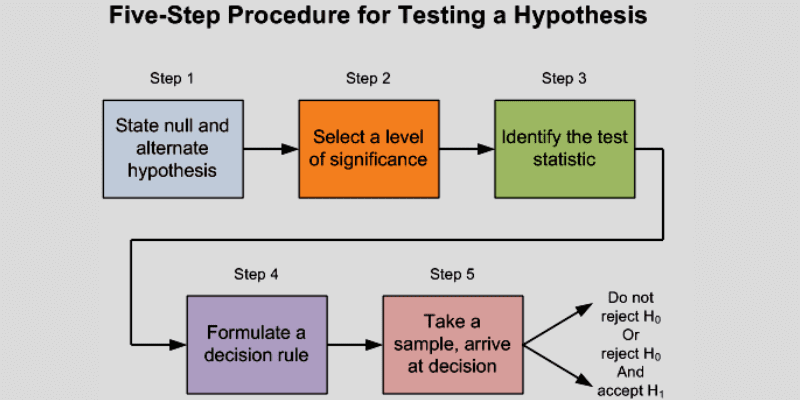
Etapas para executar o teste de hipótese
Fonte: Médio
O teste de hipóteses envolve principalmente quatro etapas:
- Defina as hipóteses: na primeira etapa, seu trabalho como analista é definir as duas hipóteses para que apenas uma seja verdadeira. A hipótese nula indicará que não há diferença na média do IMC, enquanto a hipótese alternativa afirmará que há uma diferença significativa na média do IMC.
- Planejar: Na próxima etapa, você precisará criar um plano de análise sobre como analisar os dados da amostra. É vital que você faça amostragem e colete os dados da amostra para garantir que eles sejam projetados para testar sua hipótese.
- Analisar dados de amostra: Depois de decidir como você avaliará os dados, é hora de começar o processo. Você terá que analisar os dados de amostra fisicamente para que não haja redundância. Ao analisar os dados, você deve verificar se as amostras são independentes umas das outras e se os dois tamanhos de amostra são grandes o suficiente.
- Calcular estatísticas de teste: nesta etapa, você terá que calcular as estatísticas de teste e encontrar o valor-p. O valor-p será determinado assumindo que a hipótese nula é verdadeira.
- Avalie o resultado: Na etapa final, você precisará avaliar o resultado do teste de hipótese. Aqui, você decidirá se rejeita a hipótese nula ou declara sua plausibilidade com base nos dados da amostra.
Agora, vamos explorar os benefícios do teste de hipóteses.
Benefícios do teste de hipóteses
Os benefícios do teste de hipóteses são:
- Ele ajuda você a analisar a força de sua reivindicação em uma decisão de dados.
- Como analista, permite criar um ambiente confiável para decidir sobre dados de amostra.
- Ele permite determinar se os dados de amostra envolvidos no teste de hipóteses são estatisticamente significativos.
- É benéfico para avaliar a confiabilidade e a validade dos resultados do teste em qualquer processo de teste sistemático.
Ele ajuda você a extrapolar os dados de um estágio de amostra para uma população maior, dependendo do requisito.
Casos de uso de teste de hipótese
O teste de hipóteses é utilizado em vários setores para adivinhar a precisão dos dados da amostra de forma adequada. Alguns exemplos do mundo real de testes de hipóteses são:
#1. Testes clínicos
O teste de hipóteses é amplamente utilizado durante os ensaios clínicos porque ajuda os profissionais médicos a decidir se um novo medicamento, tratamento ou procedimento será eficaz ou não com base em dados de amostra.
Um médico pode pensar que um tratamento pode aliviar os níveis de potássio em alguns pacientes. O médico pode medir o nível de potássio de um grupo de pacientes antes de fazer o tratamento e verificar o nível novamente.
Em seguida, o médico realiza o teste de hipótese onde H0: Uafter = Ubefore, e denota que o nível de potássio é o mesmo de antes após a aplicação do tratamento. Outra hipótese indica Ha: Uafter < Ubefore, significando que o nível de potássio diminuiu após a aplicação do tratamento.
Portanto, se o valor-p for menor que o nível de significância, o médico pode concluir que o tratamento pode diminuir o nível de potássio.
#2. Manufatura
O teste de hipóteses é utilizado em fábricas para ajudar os supervisores a decidir se o novo método ou técnica é eficaz ou não.
Por exemplo, algumas unidades de manufatura podem usar testes de hipóteses para descobrir se o novo método as está ajudando a reduzir o número de produtos defeituosos por lote. Suponha que o número de produtos defeituosos seja 300 por lote.
O fabricante deve determinar a média do número total de produtos defeituosos produzidos antes e depois de usar o método. Eles podem realizar testes de hipóteses e usar hipóteses H0: Uafter = Ubefore, onde a média de produtos defeituosos produzidos após a aplicação de um novo método é a mesma de antes.
Outra hipótese mostra que HA: Uafter não é igual a Ubefore, ou seja, o número total de produtos defeituosos produzidos após a aplicação do novo método não é o mesmo.
Após o teste, quando o valor-p for menor que o nível de significância, a unidade fabril pode concluir que o número de produtos defeituosos produzidos mudou.
#3. Agricultura
O teste de hipóteses é frequentemente usado para descobrir se fertilizantes ou pesticidas estão causando crescimento e imunidade nas plantas. Os biólogos podem usar o teste para provar que uma determinada planta pode crescer mais de 15 polegadas após a aplicação do novo fertilizante.
O biólogo pode aplicar o fertilizante por um mês para coletar dados de amostra. Quando o biólogo faz um teste, uma hipótese é H0 U=15 polegadas, o que indica que o fertilizante não causa aumento no crescimento médio da planta.
Outra hipótese mostra HA: U > 15 polegadas, significando que os fertilizantes causam aumento no crescimento médio da planta. Depois de testar quando o valor-p é menor que o nível de significância, o biólogo pode agora provar que os fertilizantes causam mais crescimento do que antes.
Recursos de aprendizagem
#1. Estatísticas: uma introdução passo a passo da Udemy
A Udemy está oferecendo um curso de estatística no qual você aprenderá uma introdução passo a passo à estatística, abrangendo testes de hipóteses. Este curso contém exemplos e lições de um ex-cientista de dados do Google para ajudá-lo a dominar intervalos de confiança, testes de hipóteses e muito mais.
#2. Estatísticas essenciais para análise de dados da Udemy
Este curso da Udemy sobre estatísticas essenciais para análise de dados ajudará você a aprender estatísticas com projetos do mundo real, atividades divertidas, testes de hipóteses, distribuições de probabilidade, análise de regressão e muito mais.
#3. Estatística para ciência de dados e análise de negócios
Este curso de estatística para ciência de dados e análise de negócios é oferecido pela Udemy e ajudará você a aprender o teste de hipóteses. Abrange diferentes tópicos de estatística, permitindo que cientistas de dados e analistas de negócios os aprendam e dominem. Abrange estatísticas inferenciais e descritivas juntamente com análise de regressão.
#4. Teste de Hipóteses por Jim Frost
Este livro está disponível na Amazon e é um guia intuitivo para ajudar os analistas a tomar decisões baseadas em dados.
Abrange o funcionamento dos testes de hipóteses, por que você precisa deles, como usar efetivamente intervalos de confiança, valores-p, níveis de significância e muitos outros tópicos.
#5. Teste de Hipóteses por Scott Hartshorn
Este livro é único com seus exemplos visuais e é melhor para iniciantes que buscam um guia rápido sobre testes de hipóteses.
Ele irá apresentá-lo ao significado das estatísticas, tipos e seu funcionamento. Não requer que você tenha conhecimento prévio aprofundado de estatística, mas explica tudo de forma intuitiva.
Palavra final
O teste de hipóteses ajuda a verificar uma suposição e, em seguida, desenvolver dados estatísticos com base na avaliação. Ele está sendo utilizado em muitos setores, desde manufatura e agricultura até ensaios clínicos e TI. Esse método não é apenas preciso, mas também ajuda você a tomar decisões baseadas em dados para sua organização.
A seguir, confira os recursos de aprendizado para se tornar um analista de negócios.
